fleurdejoo
Well-known member
It's a good thing you can imagine it!
Because you can't actually see it. :-(
Because you can't actually see it. :-(











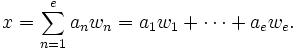
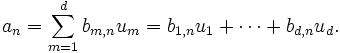
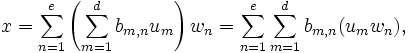
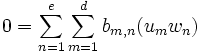
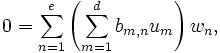
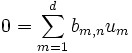
OR F2 Solve on my TI-89Also love the equations in the background.......
Suppose that K, L and M form a tower of fields as in the degree formula above, and that both d = [L:K] and e = [M:L] are finite. This means that we may select a basis {u1, ..., ud} for L over K, and a basis {w1, ..., we} for M over L. We will show that the elements umwn, for m ranging through 1, 2, ..., d and n ranging through 1, 2, ..., e, form a basis for M/K; since there are precisely de of them, this proves that the dimension of M/K is de, which is the desired result.
First we check that they span M/K. If x is any element of M, then since the wn form a basis for M over L, we can find elements an in L such that
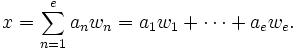
Then, since the um form a basis for L over K, we can find elements bm,n in K such that for each n,
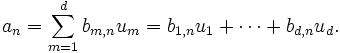
Then using the distributive law and associativity of multiplication in M we have
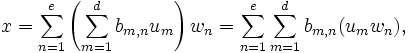
which shows that x is a linear combination of the umwn with coefficients from K; in other words they span M over K.
Secondly we must check that they are linearly independent over K. So assume that
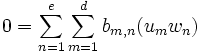
for some coefficients bm,n in K. Using distributivity and associativity again, we can group the terms as
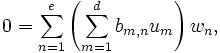
and we see that the terms in parentheses must be zero, because they are elements of L, and the wn are linearly independent over L. That is,
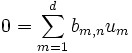
for each n. Then, since the bm,n coefficients are in K, and the um are linearly independent over K, we must have that bm,n = 0 for all m and all n. This shows that the elements umwn are linearly independent over K. This concludes the proof.
The answer is 42, Andrew.
42.
